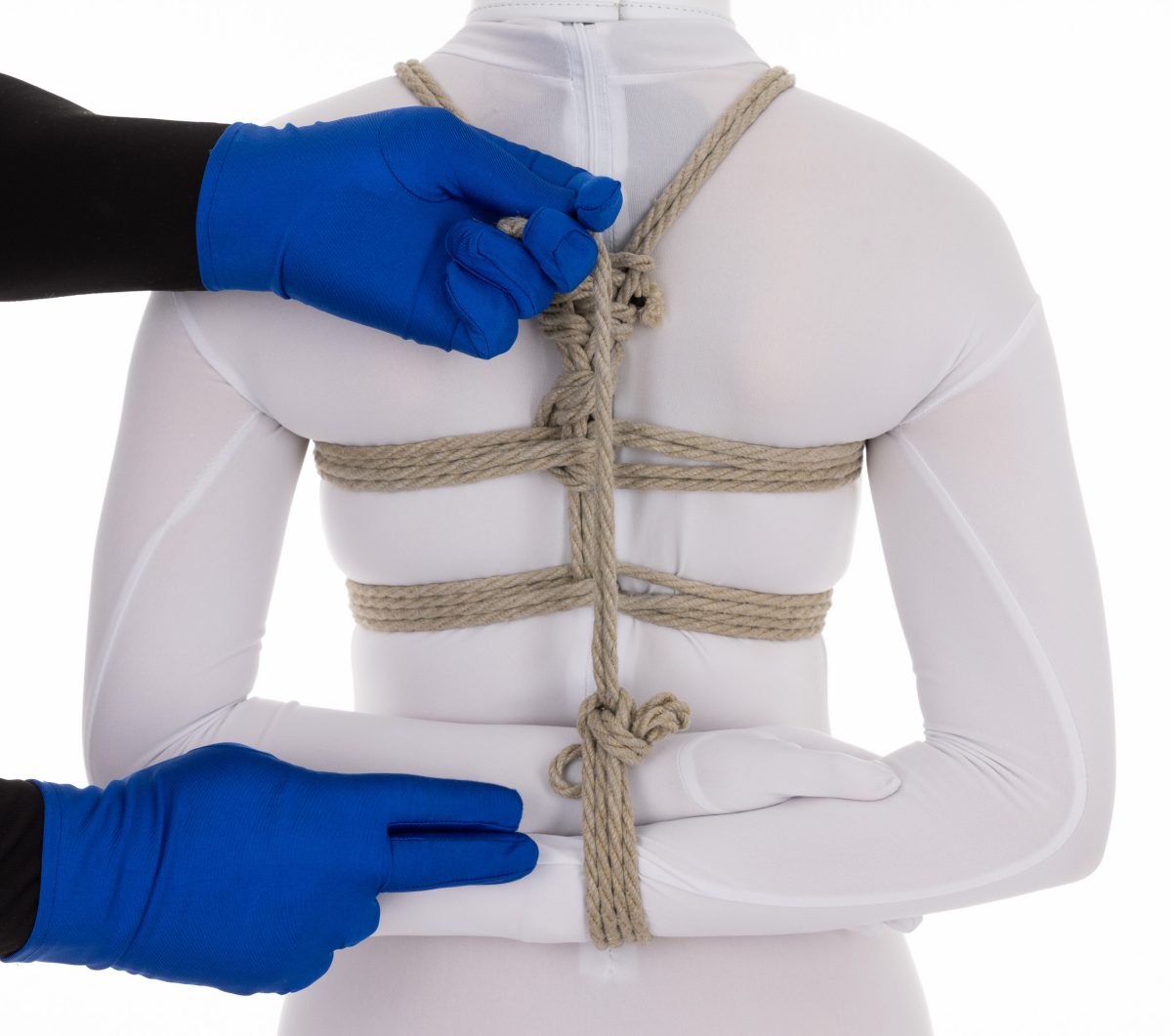
때때로 로프와 로프 주제에 대한 철학적 질문을 받곤 합니다. 예를 들어, 컬럼 타이에 관한 질문입니다:
- 하나의 커프/칸으로 된 로프이지만 두 개의 기둥이 있는 경우(예: 서머빌 보우라인으로 두 손목을 감싸는 박스 타이를 흔히 시작하는 방식) 여전히 기둥 타이인가요?
- 3열 또는 4열 넥타이 같은 것이 있나요?
이것이 제가 생각하는 방식입니다: 1-2-3열 넥타이로 만드는 것은 넥타이에 있는 개별 커프스 또는 구획의 수이지, 각 개별 구획 또는 커프스 안에 얼마나 많은 물건이 있는지가 아닙니다. .
단일 열 타이
명확한 예: a 서머빌 보우라인 한쪽 손목에 묶습니다. 분명히 단일 기둥 넥타이입니다.
동일한 기법과 동일한 구조를 사용하여 똑같은 것을 묶는다면, 단지 두 개의 기둥을 돌고 있다는 차이점이 있을 뿐입니다. 같은 것을 묶었다는 사실 자체로 같은 것이지만, 단지 두 개 이상의 기둥에 묶여 있을 뿐입니다.
때때로 사람들은 이 점에 대해 설명할 수 없을 정도로 긴장하기 때문에 다른 방식으로 예를 들어보겠습니다: 제가 서머빌 보우라인을 아무것도 없는 곳에 묶고 그 기법을 사용하여 밧줄로 커프를 만든 다음 그 커프를 테이블 위에 놓고 그것이 무엇인지 물어본다면 서머빌 보우라인이라고 대답할 것입니다. 그리고 더 자세히 설명해 달라고 요청하면 종류 였다고 말하거나 심지어는 포워드 텐션 싱글 컬럼 타이라고 말할 수도 있습니다. 현재 공기 외에는 아무것도 들어 있지 않다는 사실 때문에 0 컬럼 타이가 될 수는 없겠죠 😉.
이중 열 타이
멀티 컬럼 타이로 만들려면 여러 개의 칸이나 커프가 있도록 구조를 변경합니다.
멀티 컬럼 타이에는 보통 단일 컬럼 타이에 기둥을 구분하기 위해 신치가 추가됩니다. 예를 들어, 종달새 머리 더블 컬럼의 밴드/끈은 종달새 머리 싱글 컬럼과 같은 방식으로 형성됩니다. 유일한 차이점은 그 뒤에 오는 내용입니다. LHSC를 사용하면 하프 히치를 사용하여 잠그기만 하면 됩니다. LHDC를 사용하면 먼저 신치를 추가하여 두 개의 구획을 만든 다음 스퀘어 매듭을 사용하여 잠급니다.
이렇게 추가한 신치는 구획을 더욱 세분화합니다. 각 손목(이 예에서는)은 자체 수납공간 또는 커프에 있습니다.
이 구조가 변경되지 않으면 넥타이가 어디에 적용되고 각 칸에 몇 개의 기둥이 있는지에 관계없이 여전히 이중 기둥 넥타이입니다.
어부의 하네스에 묶인 두 사람을 상상해 보세요. 두 사람은 가슴 높이에서 묶인 양쪽 몸을 감싸는 종달새의 머리 이중 기둥을 사용하여 나란히 배치하고 서로 묶여 있습니다. 아직 사진을 찍지 못했지만 기회가 되면 사진을 찍어보겠습니다. 그때까지는 이걸로 상상해 보세요:
이들을 묶는 넥타이에는 각 칸 안에 세 개의 기둥이 있습니다: 한 사람당 가슴과 두 개의 팔이 있습니다. 그렇다고 해서 이 넥타이가 6열 넥타이가 되는 것은 아닙니다. 여전히 두 개의 칸만 있는 더블 컬럼일 뿐입니다.
트리플 컬럼 타이
이 아이디어를 확장하여 두 개 이상의 신치를 추가하여 두 개 이상의 칸을 만들어 이중 열에서 삼중 열로 만들 수 있습니다. 사실, 우리는 이미 일상적으로 이 작업을 수행하고 있습니다! 펭귄 피니언이나 고테 시바리 박스 타이에서 그 예를 볼 수 있습니다.
양쪽 팔은 하나의 로프 스트랩으로 몸에 고정하고, 양쪽에 신치를 추가하여 각 팔이 자체 커프에 고정되도록 하여 트리플 컬럼을 형성합니다.
또 다른 예로는 허리와 양쪽 허벅지에 밴드를 감은 다음 신치를 추가하여 각각 별도의 수납 공간에 넣는 도기 스타일 하네스가 있습니다.
4개 이상의 열 연결
이 아이디어를 더 확장하여 더 많은 구획을 만들기 위해 더 많은 신치를 추가할 수도 있지만, 3개 이후에는 안정성이 훨씬 떨어지는 경향이 있으므로 일반적으로는 그렇게 하지 않습니다. 이런 경우에는 더 안정적이므로 이중 기둥 시리즈를 사용하는 것이 더 일반적입니다.
예를 들어, 유연성이 좋은 사람은 발목과 손목이 모두 일렬로 또는 정사각형으로 묶이도록 묶을 수 있습니다. 하지만 이런 경우 리거가 더 자주 사용하는 방법은 각 손목을 발목에 이중 기둥으로 묶은 다음 발목을 추가로 이중 기둥으로 묶는 것입니다. 이 방법이 더 안정적인 경향이 있습니다.
즉, 철학적으로는 원한다면 이 한계를 뛰어넘을 수 있습니다!